Atom interferometers have proven very successful in precision measurements such as the determination of the fine structure constant, the determination of the Newtonian gravitational constant, and inertial sensing of gravity, gravity gradients and rotation. They also show great promise to perform general relativity tests, including the weak equivalence principle.

In parallel, atom chips provide a robust and versatile tool to trap and manipulate ultra-cold atoms, and are now routinely used in a variety of setups, including free-falling experiments in a drop tower and compact atomic clocks. In this context, they are very promising candidates for next-generation compact atomic acceleration and rotation sensors, including onboard applications. However, while a variety of integrated beam splitters and coherent manipulation techniques have been demonstrated, none of the chip-based atom interferometers developed so far has reached metrological performance. One of the initial problems encountered by atom-chip interferometers, namely the difficulty to maintain stable trapping and a reasonable trap-surface distance during the coherent splitting process, has been overcome by the use of dressed state adiabatic potentials. However, another issue remains unresolved: trapped-atom interferometers using Bose-Einstein condensates are especially sensitive to atom-atom interactions which induce phase diffusion, limiting their coherence time and putting a serious constraint on the achievable precision in the measurement of the relative phase between the two arms of the interferometer.

One possible way to reduce the interaction strength is the use of a trapped but thermal (i.e. non-degenerate) atomic cloud whose density is sufficiently low that the effect of interactions is negligible. This choice is somewhat analogous to using incoherent light in an optical interferometer.

As in a “white light interferometer”, the short coherence length of a thermal cloud (typically the thermal de Broglie wavelength) requires that the interferometer arms be kept sufficiently symmetric (in a sense that the shape difference between the two traps realizing the interferometer arms must as close as possible to zero [1]) in order to observe any interference. For example, considering a thermal gas of atom at a temperature 𝑇, if the two trapping potentials are harmonic with a curvature difference of 𝛿𝜔 which is small compare to the mean of curvature 𝜔, the contrast decay time is given by:

𝑡𝑐 = (1/𝛿𝜔) (ℏ𝜔/𝑘𝑇)

where 𝑘 is the Boltzmann constant. We checked experimentally this law in reference [2] and show some results in the following figure:

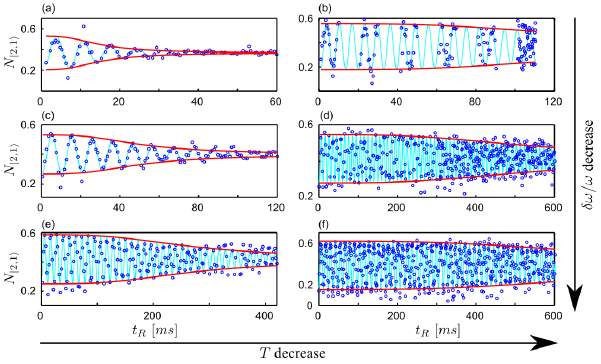
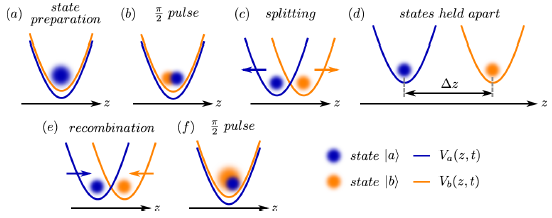
In [3] we proposed a protocol for a symmetric atom interferometer suitable for thermal atoms, using internal state labeling and adiabatic microwave dressed potentials. This protovol use two microwave frequencies on two separate coplanar waveguides, each one interacting with one (and only one) of the two internal states involved in the interferometer (namely |a>=|F=1,mF=-1> and |b>=|F=2,mF=1> of 87 rubidium).

This interferometer works as a Ramsay atomic clock except that the two states of the Ramsey interferometer are spatially split just after the first pi/2 pulse and merge just before the second pi/2 pulse. For example, to measure acceleration, which is the exemple displayed of the following figure, the two states |a> and |b> are split along a straight line [1], thus the typical sequence is as follows: the atomic cloud is prepared in state |a> and a first pi/2-pulse puts the atoms in a coherent superposition of the two states |a> and |b>. The two trapping potentials V|a>(r) (created by the first microwave frequency) and V|b>(r) (created by the second microwave frequency) are moved to spatially separate the two states, then the two states are held apart allowing the Ramsey interferometer to be sensitive to differences of potential acceleration energy. After the two trapping potentials V|a>(r) and V|b>(r) are moved to spatially recombine the two states and a second pi/2-pulse closes the interferometer. This protocol could be adapted to measure rotation [5].

References

[1] M. Dupont-Nivet, C. I. Westbrook, S. Schwartz, Contrast and phase-shift of a trapped atom interferometer using a thermal ensemble with internal state labelling, New J. Phys., 18, 113012 (2016)

[2] M. Dupont-Nivet, R. Demur, C. I. Westbrook, S. Schwartz, Experimental study of the role of trap symmetry in an atom-chip interferometer above the Bose-Einstein condensation threshold, New J. Phys., 20, 043051 (2018)

[3] M. Ammar, M. Dupont-Nivet, L. Huet, J.-P. Pocholle, P. Rosenbusch, I. Bouchoule, C. I. Westbrook, J. Estève, J. Reichel, C. Guerlin, S. Schwartz, Symmetric microwave potentials for interferometry with thermal atoms on a chip, Phys. Rev. A, 91, 053623 (2015)

[4] M. Dupont-Nivet, C. I. Westbrook, S. Schwartz, Effect of trap symmetry and atom-atom interactions on a trapped-atom interferometer with internal state labelling, Phys. Rev. A, 103, 023321 (2021)

[5] M. Dupont-Nivet, S. Schwartz, On-chip trapped ultracold atom sensor allowing rotational velocity to be measured, US10375813B2